Probability Tree Diagram

This note deals with the relationship between the intuitive approach to conditional probability being tree diagrams, and how this intuition relates to bayes' theorem and the law of total probability.

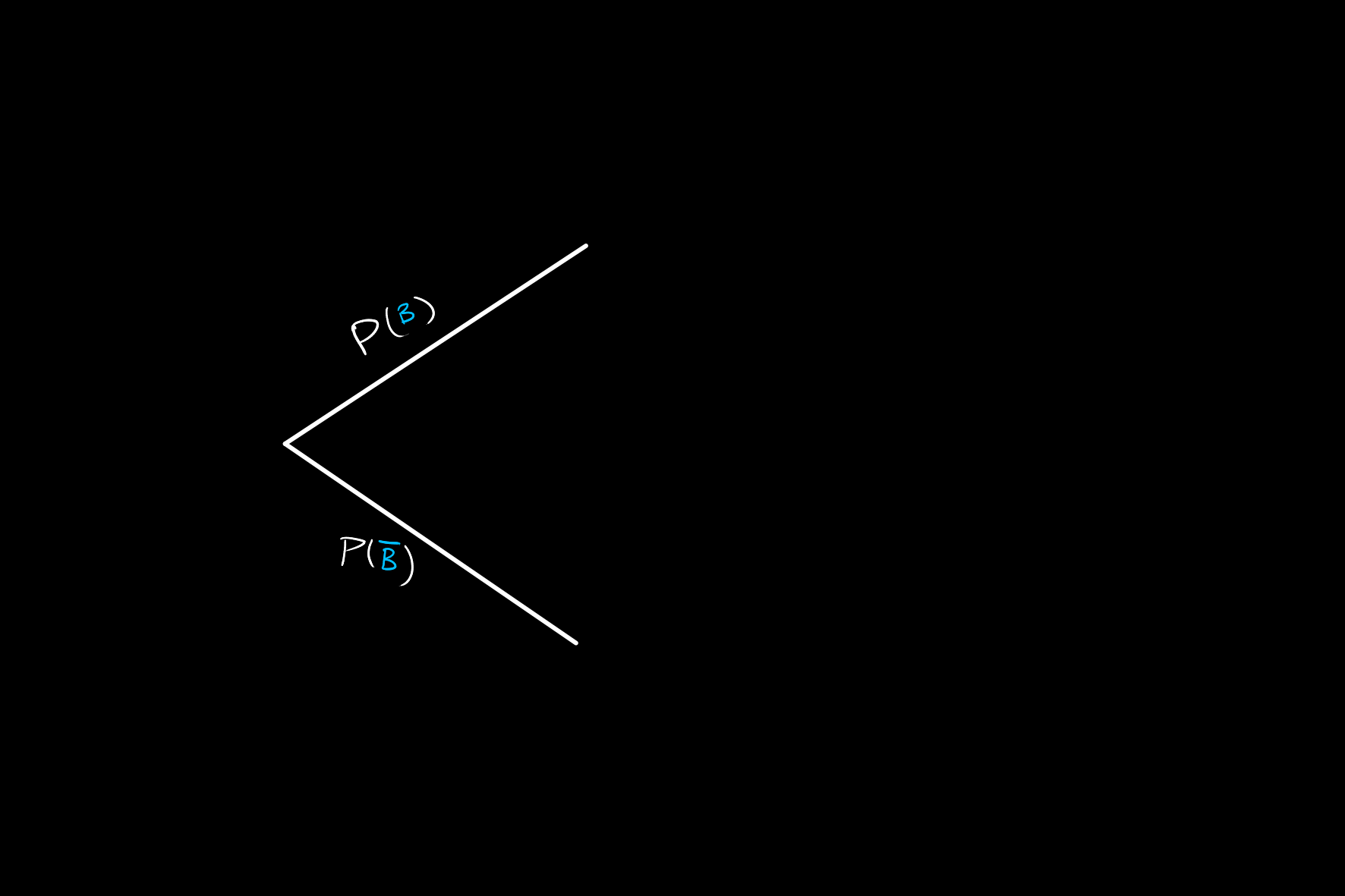
Consider events $A$ and $B$ in the same probability space. A tree diagram is typically drawn by first considering event $A$ as two cases, representing two branches on the left, where $A$ occurs and where it doesn't, with the corresponding probabilities drawn on those branches:

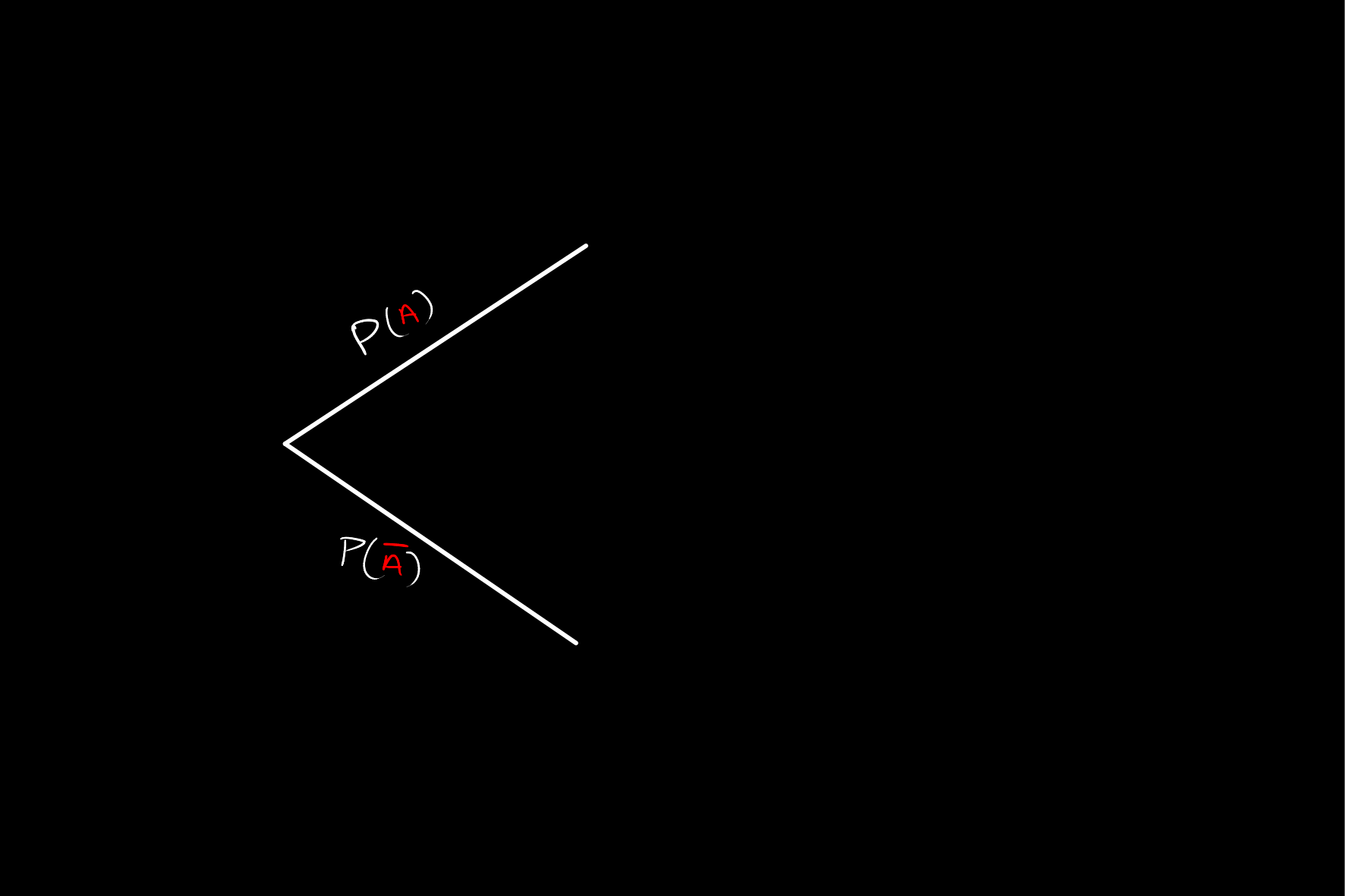
Now, in each of these cases we have two possible states for event $B$, and so we draw these on in the same way, branching out from the cases for $A$:

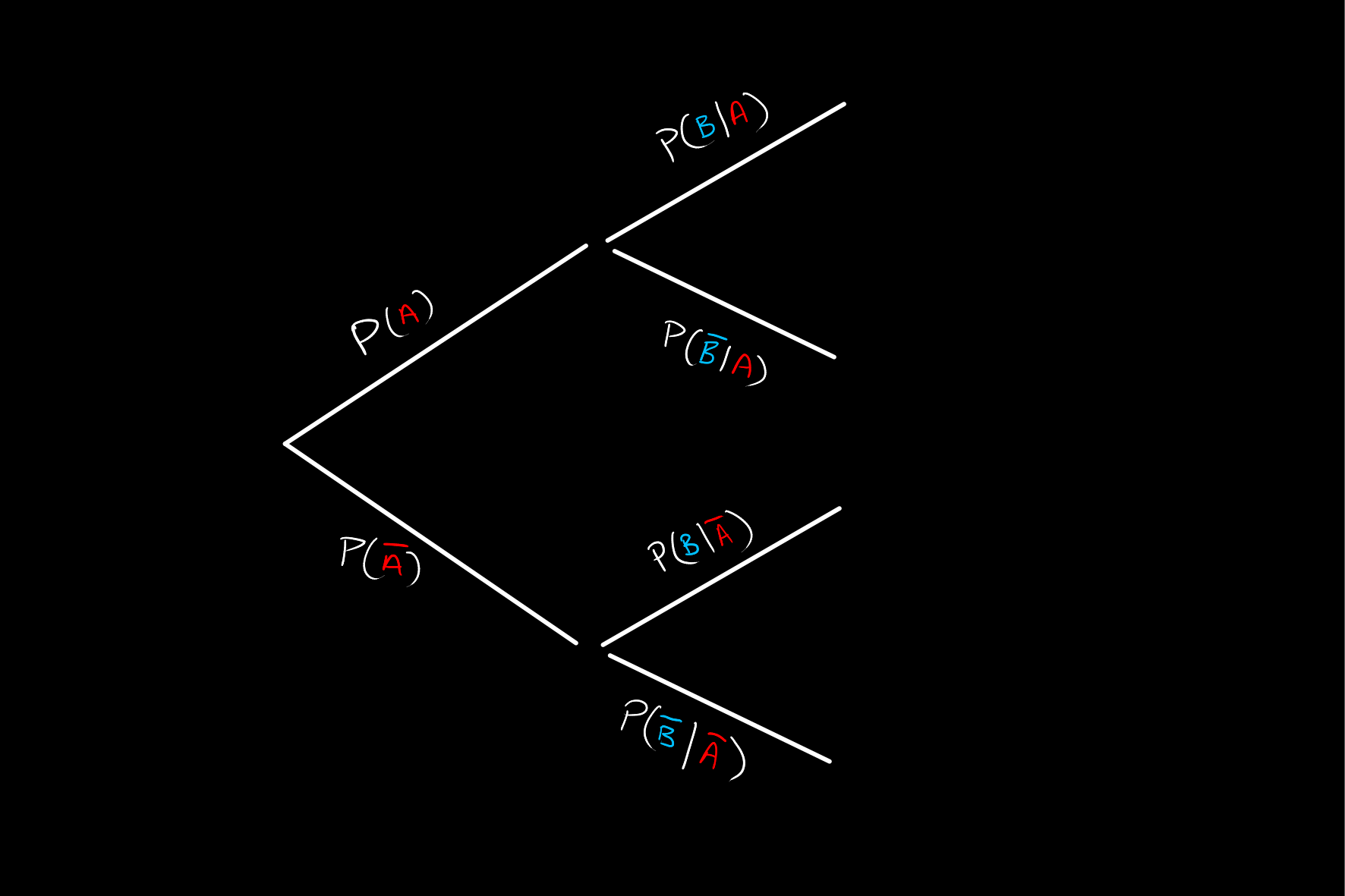
This then gives all possible states for $A$ and $B$ as the $4$ end points. As such, we can write the probabilities of each of these four cases using the multiplicative rule of probability by multiplying down the branches:

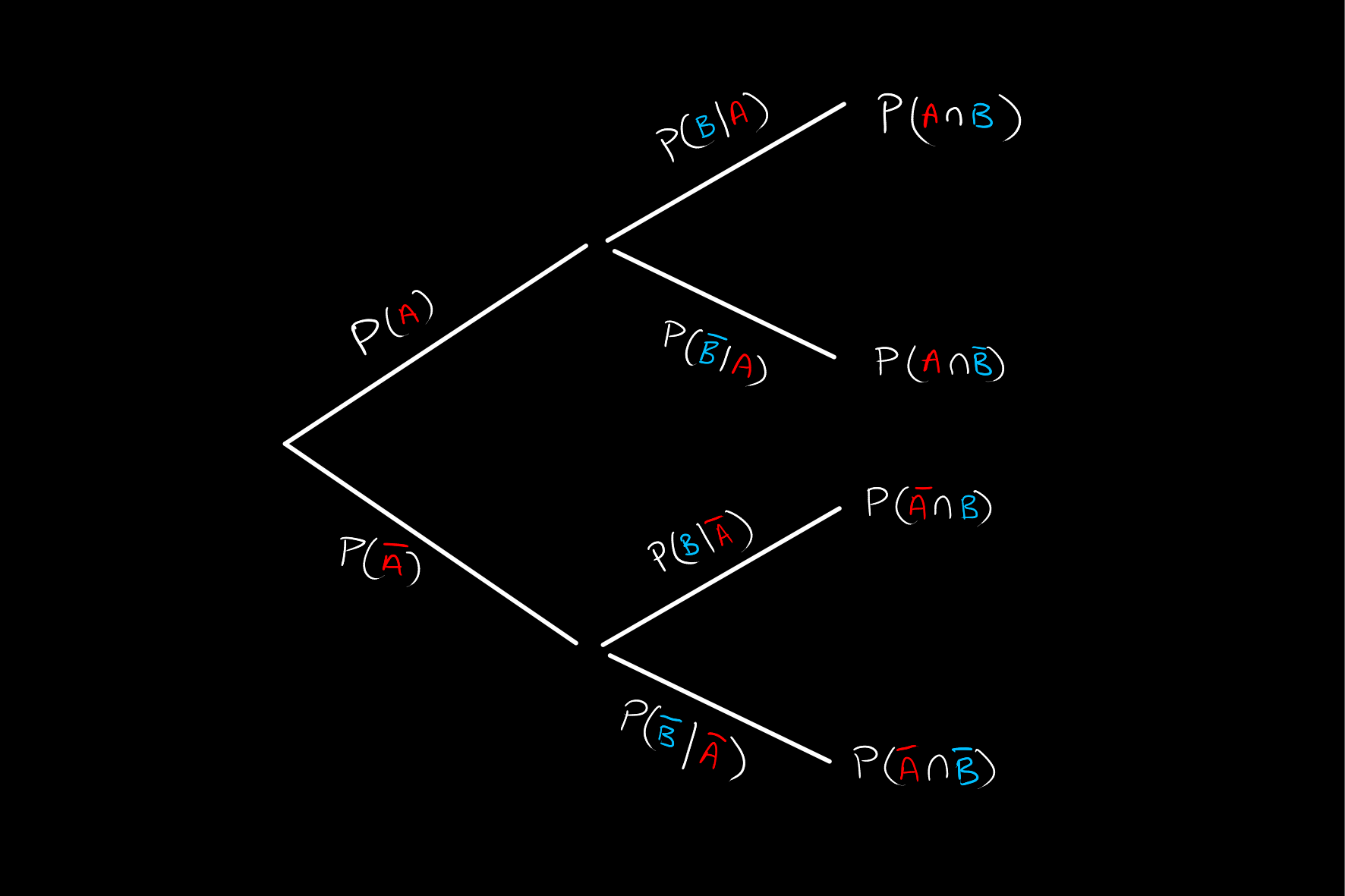
Now that this tree diagram has been drawn out, we may use to calculate other probabilities not listed here. The first useful thing to know would be the probability of $B$ occurring. This is just a consequence of summing up the cases on the end in which $B$ occurs:

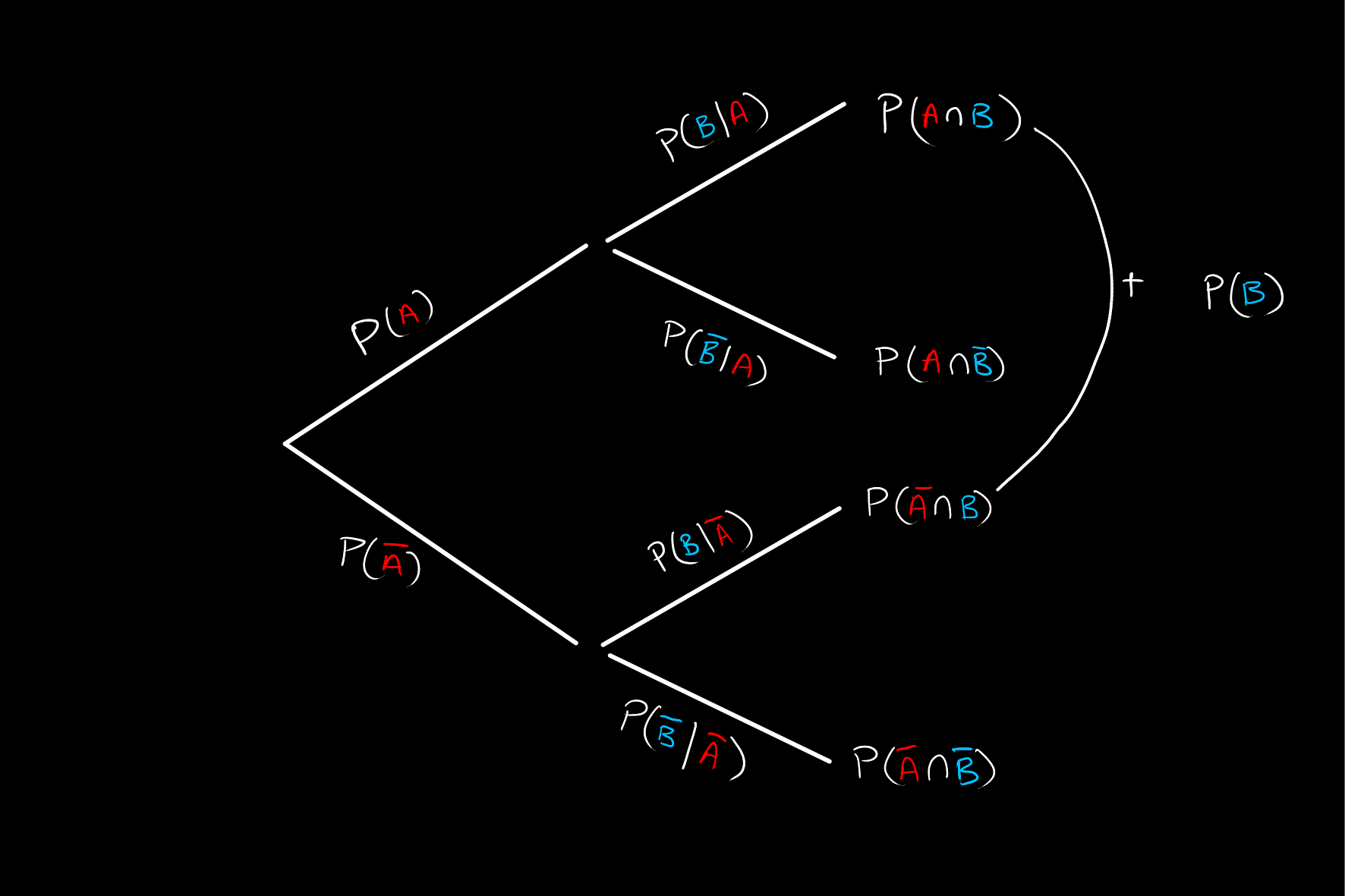
We may do this given that all four cases at the end are mutually exclusive.

This addition is just an application of the law of total probability. That is, we are calculating:

The other useful probabilities we may wish to know are the probabilities of $A$ conditional on $B$. This is equivalent to redrawing our tree diagram in reverse, with $B$ first. This first stage is easy given that we now know $P(B)$ and hence $P(\bar{B})$ from the probability of complementary events:

The remaining probabilities we need to complete this diagram follow from Baye's theorem. For example, on the first branch we need:

where $P(B\mid A)$ and $P(A)$ appear on our first tree diagram, and $P(B)$ appears on the first part of our current diagram. Completing this we end up with a tree diagram like this:

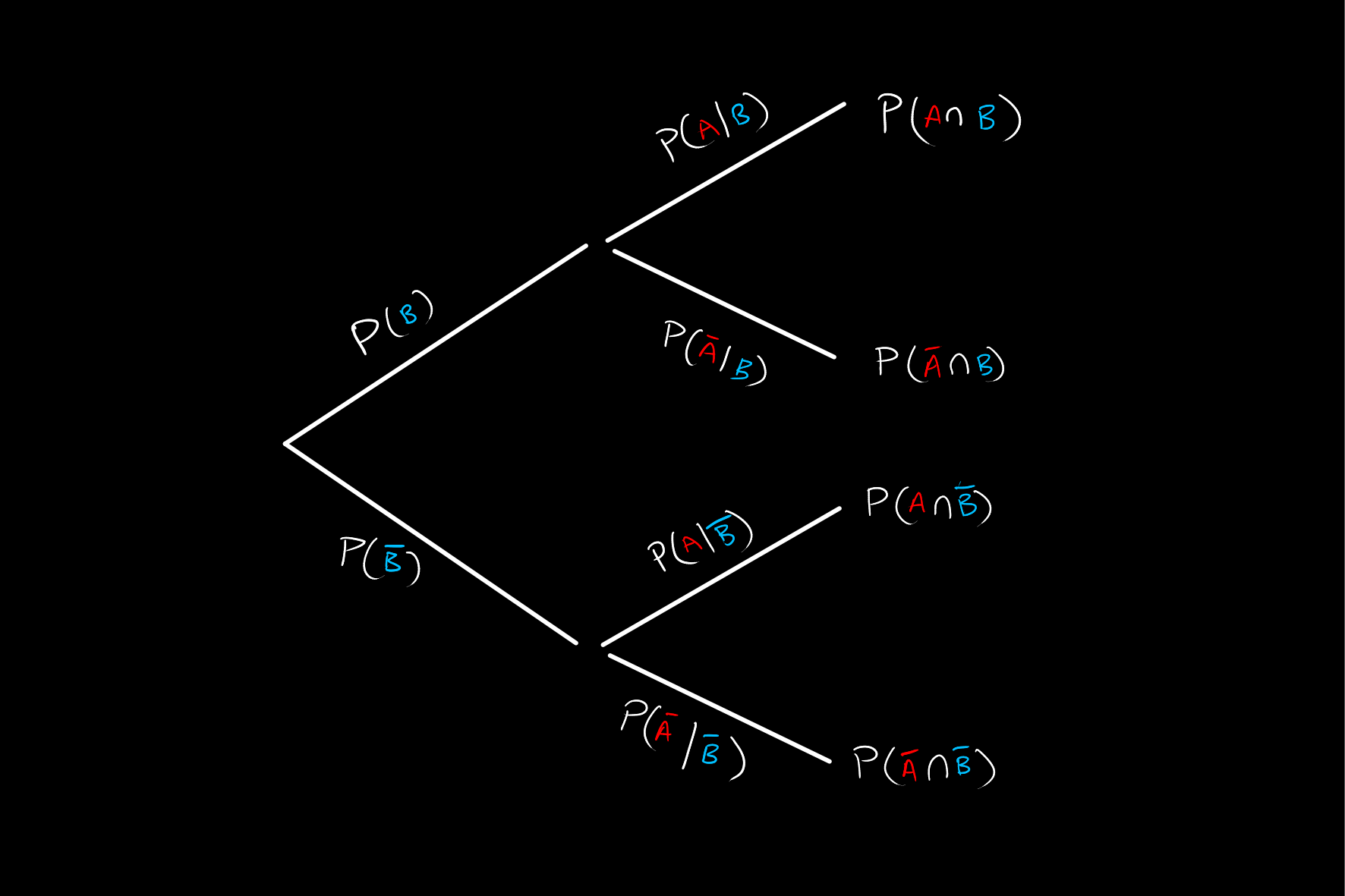
noting that the probabilities on the far right are just a permutation of those we had on the first tree diagram.